Если вы являетесь специалистом по SEO или цифровым маркетологом, читая эту статью, возможно, вы экспериментировали с искусственным интеллектом и чат-ботами в своей повседневной работе.
Но вопрос в том, как можно максимально эффективно использовать возможности ИИ, кроме использования пользовательского интерфейса чат-бота?
Для этого вам необходимо глубокое понимание того, как работают большие языковые модели (LLM), и изучить базовый уровень кодирования. И да, программирование в наши дни абсолютно необходимо для успеха в качестве профессионала в области SEO.
Это первый из серия статей которые направлены на повышение вашего уровня навыков, чтобы вы могли начать использовать LLM для масштабирования своих задач SEO. Мы верим, что в будущем этот навык понадобится для достижения успеха.
Нам нужно начать с азов. Он будет включать важную информацию, поэтому позже в этой серии вы сможете использовать LLM для масштабирования своих SEO или маркетинговых усилий для решения самых утомительных задач.
В отличие от других подобных статей, которые вы читали, здесь мы начнем с конца. Видео ниже показывает, что вы сможете сделать после прочтения всех статей серии о том, как использовать LLM для SEO.
Наша команда использует этот инструмент, чтобы ускорить внутренние ссылки, сохраняя при этом человеческий контроль.
Тебе понравилось? Это то, что вы сможете построить сами очень скоро.
Теперь давайте начнем с основ и предоставим вам необходимые базовые знания в области LLM.
Что такое векторы?
В математике векторы — это объекты, описываемые упорядоченным списком чисел (компонентов), соответствующих координатам в векторном пространстве.
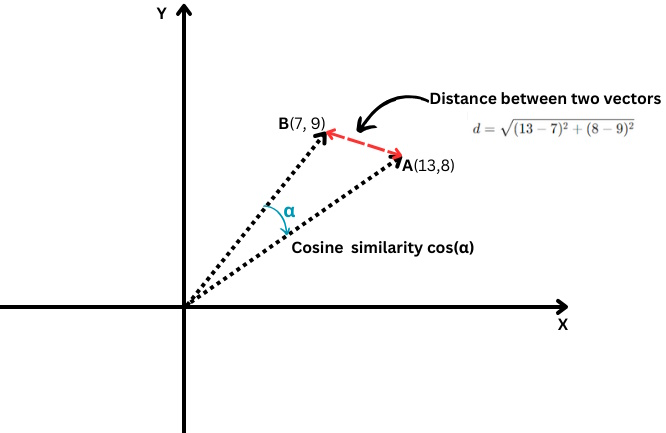
Простым примером вектора является вектор в двумерном пространстве, который обозначается (x,y). координаты, как показано ниже.
В этом случае координата x=13 представляет длину проекции вектора на ось X, а y=8 представляет длину проекции вектора на ось Y.
Векторы, определяемые координатами, имеют длину, которая называется величиной вектора или нормой. Для нашего двумерного упрощенного случая он рассчитывается по формуле:
Однако математики пошли дальше и определили векторы с произвольным числом абстрактных координат (X1, X2, X3… Xn), что называется «N-мерный» вектор.
В случае вектора в трехмерном пространстве это будут три числа (x,y,z), которые мы все еще можем интерпретировать и понимать, но все, что выше этого, находится за пределами нашего воображения, и все становится абстрактным понятием.
И здесь в игру вступают встраивания LLM.
Что такое встраивание текста?
Вложения текста — это подмножество вложений LLM, которые представляют собой абстрактные многомерные векторы, представляющие текст, который фиксирует семантические контексты и отношения между словами.
На жаргоне LLM «слова» называются токенами данных, причем каждое слово является токеном. Более абстрактно, внедрения — это числовые представления этих токенов, кодирующие отношения между любыми токенами данных (единицами данных), где токен данных может быть изображением, звукозаписью, текстом или видеокадром.
Чтобы посчитать, насколько слова близки семантически, нам необходимо преобразовать их в числа. Точно так же, как вы вычитаете числа (например, 10-6=4) и можете определить, что расстояние между 10 и 6 составляет 4 балла, можно вычесть векторы и вычислить, насколько близки эти два вектора.
Таким образом, понимание векторных расстояний важно для понимания того, как работают LLM.
Существуют разные способы измерения близости векторов:
- Евклидово расстояние.
- Косинусное подобие или расстояние.
- Сходство Жаккара.
- Манхэттенское расстояние.
У каждого из них есть свои варианты использования, но мы обсудим только часто используемые косинус и евклидовы расстояния.
Что такое косинусное подобие?
Он измеряет косинус угла между двумя векторами, т. е. насколько близко эти два вектора совпадают друг с другом.
 Евклидово расстояние против косинусного подобия
Евклидово расстояние против косинусного подобияОно определяется следующим образом:
Где скалярное произведение двух векторов делится на произведение их величин, то есть длин.
Его значения варьируются от -1, что означает совершенно противоположное, до 1, что означает идентичность. Значение «0» означает, что векторы перпендикулярны.
Что касается встраивания текста, достижение точного значения косинусного сходства -1 маловероятно, но вот примеры текстов с косинусным сходством 0 или 1.
Косинусное сходство = 1 (идентично)
- «10 лучших скрытых жемчужин Сан-Франциско для индивидуальных путешественников»
- «10 лучших скрытых жемчужин Сан-Франциско для индивидуальных путешественников»
Эти тексты идентичны, поэтому их вложения будут одинаковыми, что приведет к косинусному сходству, равному 1.
Косинусное сходство = 0 (перпендикулярно, что означает отсутствие связи)
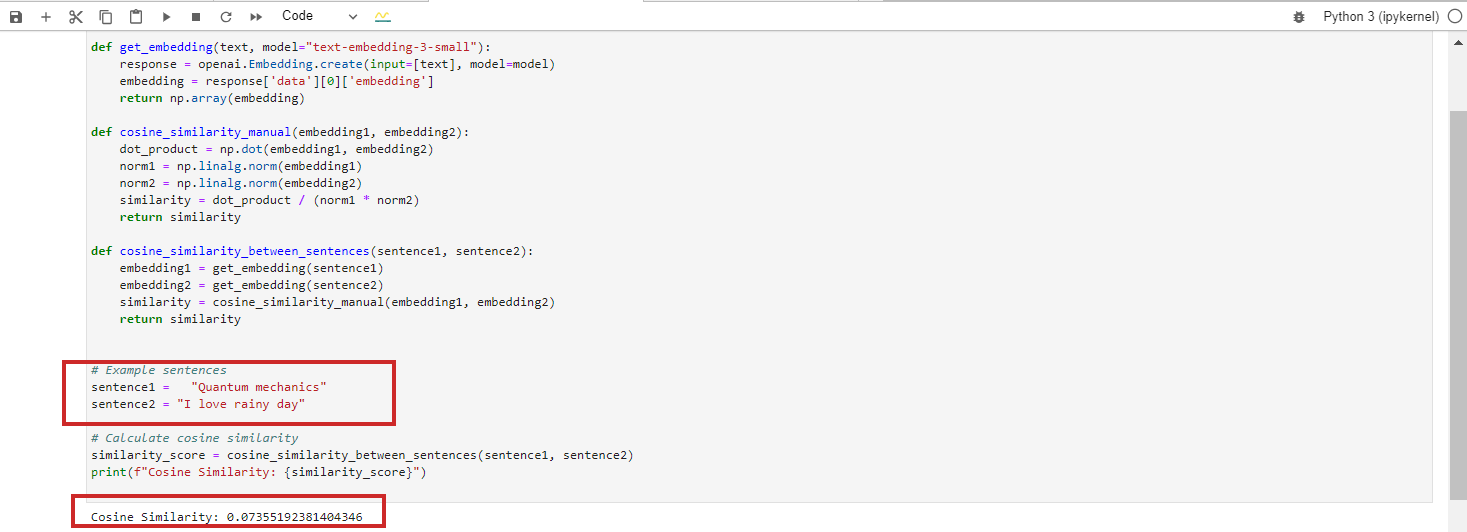
- «Квантовая механика»
- «Я люблю дождливый день»
Эти тексты совершенно не связаны, в результате чего косинусное сходство между их текстами равно 0. БЕРТ вложения.
Однако если вы запустите модель внедрения Google Vertex AI 'text-embedding-preview-0409', вы получите 0,3. С OpenAi 'встраивание текста-3-большой' модели, вы получите 0,017.
(Примечание: в следующих главах мы подробно научимся работать с встраиваниями с использованием Python и Юпитер).
Модель Vertex Ai text-'embedding-preview-0409'
Модель OpenAi «text-embedding-3-small»
Мы опускаем случай с косинусным подобием = -1, потому что это маловероятно.
Если вы попытаетесь получить косинусное сходство для текста с противоположными значениями, например «любовь» и «ненависть» или «успешный проект» и «неудачный проект», вы получите косинусное сходство 0,5–0,6 с Google Vertex AI. 'text-embedding-preview-0409' модель.
Это потому, что слова «любовь» и «ненависть» часто встречаются в схожих контекстах, связанных с эмоциями, а слова «успешный» и «неудачный» связаны с результатами проекта. Контексты, в которых они используются, могут существенно перекрываться в обучающих данных.
Косинусное сходство можно использовать для следующих SEO-задач:
- Классификация.
- Кластеризация ключевых слов.
- Реализация перенаправлений.
- Внутренняя перелинковка.
- Обнаружение дублированного контента.
- Рекомендация по контенту.
- Анализ конкурентов.
Косинусное подобие фокусируется на направлении векторов (угол между ними), а не на их величине (длине). В результате он может уловить семантическое сходство и определить, насколько близко совпадают два фрагмента контента, даже если один из них намного длиннее или использует больше слов, чем другой.
Глубокое погружение и изучение каждого из них будет целью предстоящие статьи мы опубликуем.
Что такое евклидово расстояние?
Если у вас есть два вектора A(X1,Y1) и B(X2,Y2), Евклидово расстояние рассчитывается по следующей формуле:
Это похоже на использование линейки для измерения расстояния между двумя точками (красная линия на графике выше).
Евклидово расстояние можно использовать для следующих SEO-задач:
- Оценка плотности ключевых слов в контенте.
- Поиск дублированного контента со схожей структурой.
- Анализ распределения анкорного текста.
- Кластеризация ключевых слов.
Вот пример расчета евклидова расстояния со значением 0,08, что почти близко к 0, для дублированного контента, в котором абзацы просто заменены местами — это означает, что расстояние равно 0, т. е. контент, который мы сравниваем, один и тот же.
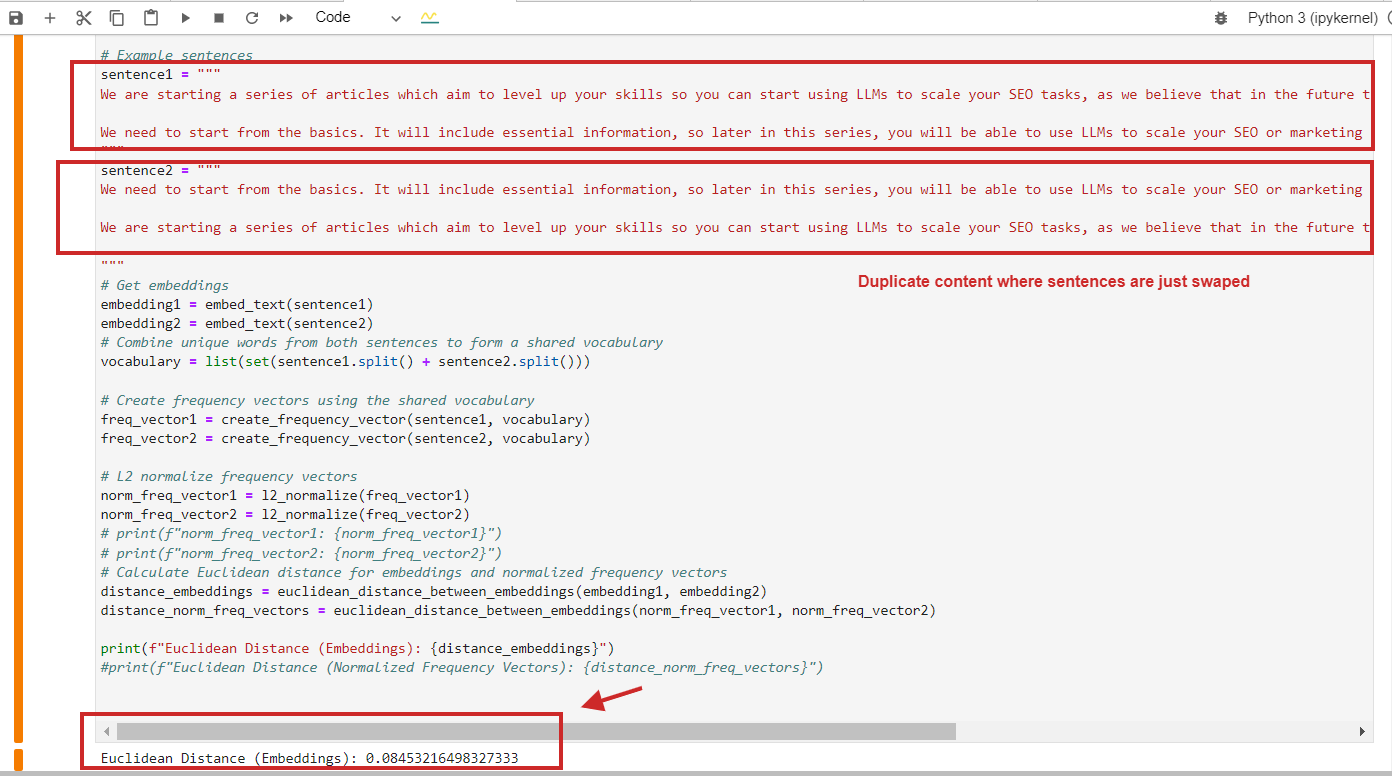 Пример расчета евклидова расстояния для повторяющегося контента
Пример расчета евклидова расстояния для повторяющегося контентаКонечно, вы можете использовать косинусное сходство, и оно обнаружит дублированный контент с косинусным сходством 0,9 из 1 (почти идентично).
Вот ключевой момент, который следует запомнить: вам следует полагаться не только на косинусное подобие, но и использовать другие методы, например: Исследовательская работа Netflix предполагает, что использование косинусного сходства может привести к бессмысленному «сходству».
Мы показываем, что косинусное подобие изученных вложений на самом деле может давать произвольные результаты. Мы обнаруживаем, что основная причина заключается не в косинусном подобии как таковом, а в том факте, что изученные вложения обладают некоторой степенью свободы, которая может отображать произвольные косинусные подобия.
Как профессионалу в области SEO, вам не обязательно полностью понимать эту статью, но помните, что исследования показывают, что другие дистанционные методы, такие как евклидов, следует рассматривать в зависимости от потребностей проекта и результатов, которые вы получаете, чтобы уменьшить количество ложных результатов. положительные результаты.
Что такое нормализация L2?
Нормализация L2 — это математическое преобразование, применяемое к векторам, чтобы сделать их единичными векторами длиной 1.
Чтобы объяснить простыми словами, предположим, что Боб и Алиса прошли большое расстояние. Теперь мы хотим сравнить их направления. Шли ли они одинаковыми путями или пошли совершенно в разных направлениях?
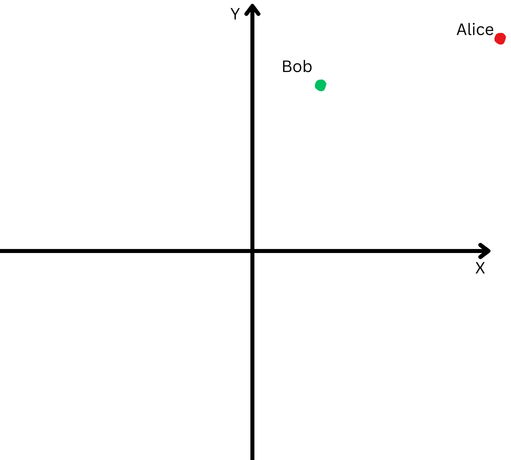 «Алиса» представлена красной точкой в правом верхнем квадранте, а «Боб» — зеленой точкой.
«Алиса» представлена красной точкой в правом верхнем квадранте, а «Боб» — зеленой точкой.Однако, поскольку они находятся далеко от места своего происхождения, нам будет сложно измерить угол между их траекториями, поскольку они зашли слишком далеко.
С другой стороны, мы не можем утверждать, что если они далеко друг от друга, значит, их пути разные.
Нормализация L2 подобна возвращению Алисы и Боба на одинаковое расстояние от начальной точки, скажем, на один фут от начала координат, чтобы облегчить измерение угла между их путями.
Теперь мы видим, что, хотя они и далеко друг от друга, направления их пути довольно близки.
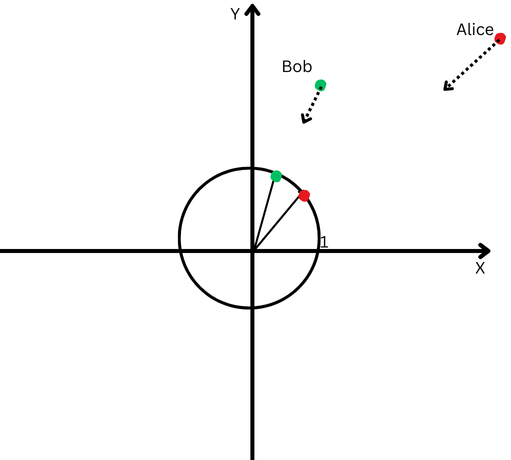 Декартова плоскость с кругом в начале координат.
Декартова плоскость с кругом в начале координат.Это означает, что мы устранили влияние их различной длины пути (так называемой величины векторов) и можем сосредоточиться исключительно на направлении их движения.
В контексте встраивания текста эта нормализация помогает нам сосредоточиться на семантическом сходстве между текстами (направлении векторов).
Большинство моделей внедрения, таких как модели «text-embedding-3-large» от OpeanAI или модели «text-embedding-preview-0409» от Google Vertex AI, возвращают предварительно нормализованные представления, что означает, что вам не нужно нормализовать.
Но, например, модель BERT 'bert-base-без корпуса' вложения не являются предварительно нормализованными.
Заключение
Это была вводная глава нашей серии статей, призванная познакомить вас с жаргоном студентов-магистров права, что, я надеюсь, сделало информацию доступной без необходимости иметь докторскую степень по математике.
Если у вас все еще есть проблемы с их запоминанием, не волнуйтесь. При рассмотрении следующих разделов мы будем обращаться к определениям, определенным здесь, и вы сможете понять их на практике.
Следующие главы будут еще интереснее:
- Введение в встраивание текста OpenAI с примерами.
- Введение в встраивание текста Google Vertex AI с примерами.
- Введение в векторные базы данных.
- Как использовать встраивания LLM для внутренних ссылок.
- Как использовать встраивания LLM для масштабной реализации перенаправлений.
- Собираем все вместе: плагин WordPress на основе LLM для внутренних ссылок.
Цель — повысить уровень ваших навыков и подготовить вас к решению проблем в области SEO.
Многие из вас могут сказать, что есть инструменты, которые можно купить, которые выполняют подобные действия автоматически, но эти инструменты не смогут выполнять многие конкретные задачи, основанные на потребностях вашего проекта, которые требуют индивидуального подхода.
Использовать инструменты SEO — это всегда здорово, но иметь навыки — еще лучше!
Дополнительные ресурсы:
Рекомендованное изображение: Krot_Studio/Shutterstock